
Science & You
BVIS HANOI (VV)
Phuong & Chi


hysteresis loop ( for polymeric materials - check below)

energy stored
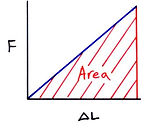
* Tough material requires a large energy before breaking (i.e big area under the graph)
Area under the force - extension graph = work done in stretching the spring
=> This is stored as elastic potential energy (EPE)
EPE = 1/2 Fx = 1/2 kx^2
When the force is removed from a material it will contract. For some materials it will return to its original length but via a different route on the Force - Extension graph.
Area between the lines is the different in energy between loading and unloading = heat loss during 1 loading, unloading cycle
brittle materials
Stress = Force/ Cross sectional Area
σ (sigma) is a symbol for stress, has a unit of Nm^-2
Strain = extension/ original length
ε is a symbol for strain, has no unit
Young's modulus = stress/strain = F/A x L/x
Unit: Pa (Nm^-2)
interesting force - extension graphs

stress - strain - young's modulus
force - extension graph
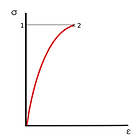
Area under the σ - ε graph
=> σ x ε =F/A x x/L = Area/ Volume = Energy stored/ Volume of the material
Energy stored per unit volume
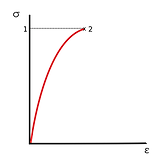
The gradient of the straight section is the Young's modulus
stell
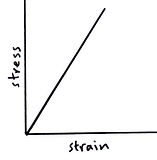
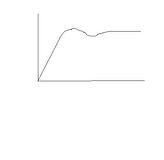
Brittle materials have no (or very little) plastic region to their graph and so their graph is just a straight line until breaking with a very small deformation
Steel is an alloy of iron and carbon. Mid steel contains mainly iron. It has an interesting F-x graph due to the arrangement of atoms in its structure
polymeric materials


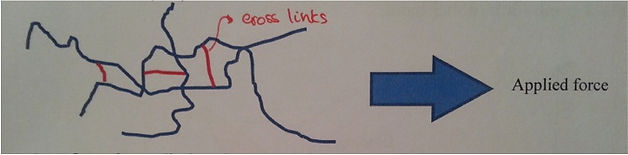

A polymer is a maerial which is manufactured from very long chains of atoms called molecules. Initially these long polymer chains (blue) are randomly arranged can be cross linked (red)
As a force is applied to the material the cross links are stretched. This gives rise to a small elastic deformation
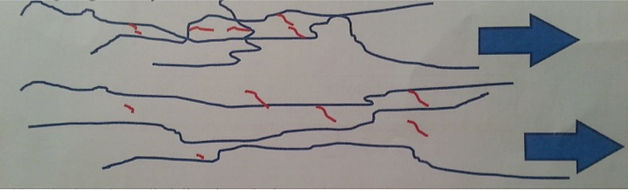
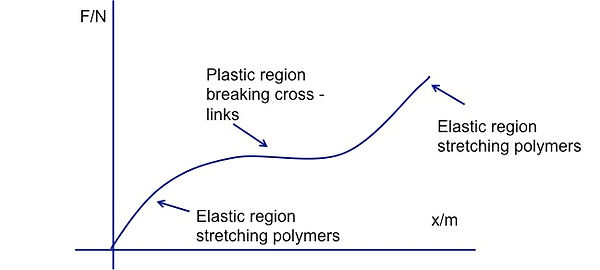
As more force is applied the cross links start to break. This gives rise to a permanent plastic deformation. The long chains start to straightne out and the material increases in length significantly
Now the force is applied directly to the long polymer molecules and it returns to an elastic region
As a result the polymer has two regions of elastic deformation with a plastic deformation in between
experiment


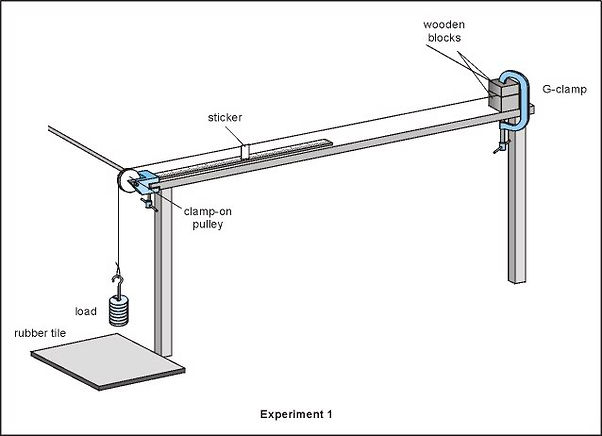
Measurements:
Initial length
Force/ Weight
Diameter
(Extension)
Equipment
Meter ruler
Micrometer/ Screw gauge/ Vernier scale
Calculate
Cross sectional area
A = πr^2 = π(d/2)^2 = d^2 x π/4
Graph

gradient = σ/ ε = Young's modulus

